Dans cette section sont présentées les méthodes de Chimiométrie et de Machine Learning les plus connues et les plus couramment utilisées :
-
Les méthodes d’analyse exploratoire
Analyse en Composantes Principales
L’Analyse en Composantes Principales ou ACP est une des méthodes les plus utilisées en chimiométrie. Cette méthode est utilisée pour les objectifs suivants :
- La visualisation des données dans l’espace multivarié
- La détection de clusters
- L’effet de facteurs de variabilité
- La détection d’échantillons atypiques (outliers)
- La compression des données, en réduisant la dimensionnalité de X
- La suppression de bruit
L’ACP permet de visualiser des échantillons représentés par de nombreuses variables, en projetant leurs coordonnées d’origine dans un nouvel ensemble d’axes, appelés composantes principales (CP). Ces axes sont construits de façon à maximiser la variance de X, extrayant ainsi l’information présente dans X. Les k premières composantes représentent l’information résumée de X, les dernières composantes représentent le bruit. Les graphiques présentés ci-contre expliquent comment l’ACP fonctionne pour une matrice X simple, composée de seulement trois variables.
L’ACP peut être considérée comme un changement d’axes, conçus pour mieux visualiser la variabilité des échantillons, tout en maintenant les distances et les échelles entre les échantillons. Pour simplifier la visualisation, les échantillons sont habituellement observés sur un plan 2D ou 3D, correspondant à la projection des échantillons sur un ensemble de 2 ou 3 axes.
L’ACP peut être également la première étape pour d’autres méthodes multivariées, telles que la classification non supervisée ou la maîtrise statistique des procédés (MSPC) .
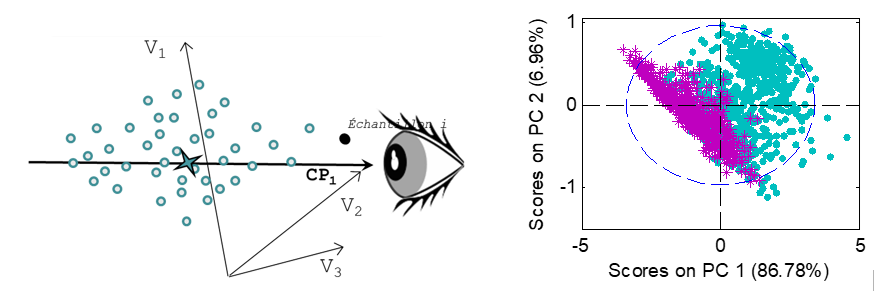
Analyse Multi-blocs
L’analyse de données multi-blocs permet de traiter des ensembles de données dans lesquels :
- les mêmes échantillons sont caractérisés avec différents blocs de variables; la nature et le nombre de variables de ces différents blocs pouvant varier,
- ou plusieurs blocs d’échantillons sont caractérisés avec les mêmes variables, le nombre de ces échantillons dans chaque bloc pouvant être différent.
Le but des méthodes d’analyse de données multi-blocs est d’identifier des informations communes et spécifiques au sein des différents blocs de données.

Analyse en Composantes Indépendantes
L’ICA a pour objectif de répondre à la problématique d’identification des produits et phénomènes présents dans un mélange, ou lors d’un procédé. Les composantes principales d’une ACP, qui décrivent le plus souvent un mélange de ces sources pures, ne fournissent pas toujours une réponse adaptée.
L‘ICA vise à extraire les signaux sources sous-jacents de la matrice ainsi que leurs proportions dans chaque mélange mesuré.
L’hypothèse de base de l’ICA consiste à considérer chaque ligne de la matrice X, comme étant une combinaison linéaire de signaux « sources » indépendants S, avec des coefficients de Pondération, ou « proportions » A, proportionnels à la contribution des signaux sources aux mélanges correspondants.
Contrairement à l’ACP, les résultats dépendent du nombre de composantes que l’on souhaite extraire. Ainsi, pour une ICA à 3 composantes par exemple, la première composante sera différente de celle d’une ICA réalisée sur 4 composantes. Il existe des outils permettant de faciliter le choix du nombre de composantes, comme par exemple l’ICA par blocs, qui permet de vérifier la robustesse du modèle en regardant les corrélations entre les composantes de modèles ICA réalisés sur les données partagées en blocs.
-
Classification non supervisée (clustering) :
Il existe deux ensembles de méthodes de classification.
Le premier regroupe les méthodes de classification non-supervisée (ou clustering) qui visent à classer des échantillons similaires sans l’utilisation de connaissances a priori.
Le second regroupe les méthodes de classification supervisée (ou discrimination), où l’appartenance des échantillons aux différentes classes est utilisée pour construire un modèle.
Les techniques de clustering, également appelées « techniques de classification non supervisée » dans le domaine de la chimiométrie, sont des outils d’exploration qui visent à déterminer les tendances de regroupement naturelles de la structure interne des données sans aucune autre connaissance préalable sur l’affectation des échantillons à des classes. Ainsi, ces méthodes mesurent les similitudes entre les échantillons, uniquement en fonction de leurs valeurs X.
Classification Ascendante Hiérarchique (CAH)
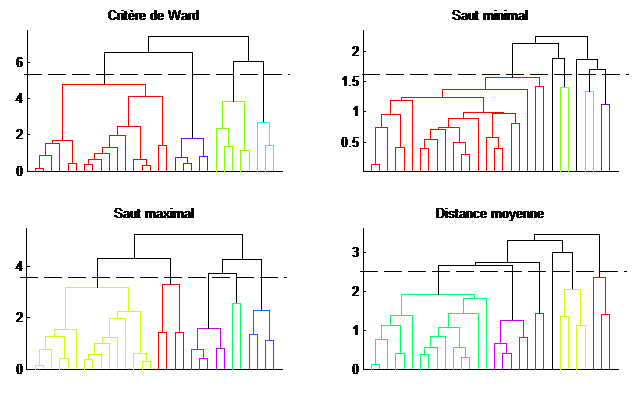
La classification hiérarchique est une méthode qui assemble ou dissocie successivement les ensembles d’échantillons. Dans la Classification Ascendante Hiérarchique (CAH), n classes sont considérées au départ, à savoir une classe par échantillon, et ces classes sont ensuite regroupées successivement jusqu’à constituer une classe unique. Le résultat est donné sous la forme d’un arbre de classification, appelé dendrogramme, où la longueur des branches représente la distance entre les groupes. Le choix des groupes finaux est décidé en coupant l’arbre à un seuil spécifique ; ainsi le nombre de clusters n’est pas un paramètre à régler à l’avance.
En revanche, deux autres critères doivent être définis : la distance entre échantillons (généralement la distance Euclidienne) et le critère de regroupement. Différents arbres sont indiqués dans la figure en fonction du critère choisi. L’impact du critère sur la classification est assez visible sur cette figure.
K-Means
Les méthodes de regroupement non hiérarchique visent à construire une partition finale des données. Contrairement à l’approche hiérarchique, l’utilisateur doit définir un nombre fixe de groupes a priori. Ce qui peut être une forte limitation à l’utilisation de ces techniques.
La méthode des K-means très répandue est une procédure itérative qui permet de trouver la partition optimale de k classes.
La partition initiale de k groupes est généralement générée au hasard. Les résultats sont très dépendants de cette partition initiale, ainsi que du choix du nombre de classes k.
Puis, à chaque itération, le barycentre de chacune des classes est recalculé et les échantillons sont réaffectés au centre le plus proche.
Cette procédure est effectuée jusqu’à ce que le critère d’arrêt soit atteint (par exemple : aucun changement d’affectation ou bien un nombre maximum d’itérations atteint).

-
Les méthodes de régression MLR, PCR, PLS :
MLR – Multiple Linear Regression
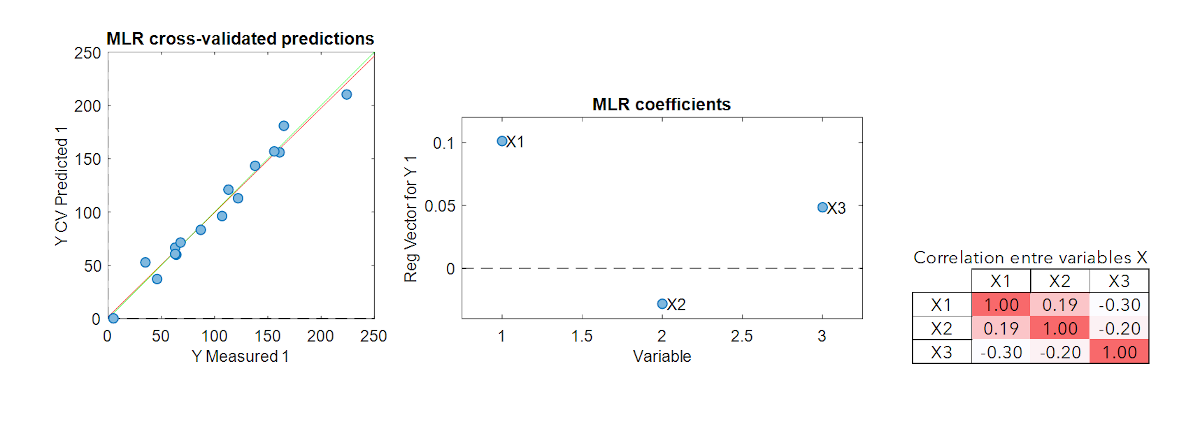
La régression linéaire multiple (MLR) est la méthode de modélisation multivariée la plus basique. C’est l’extension de la régression linéaire simple au cas multivarié.
Cette méthode a l’avantage d’être facile à mettre en oeuvre. Toutefois, si les variables explicatives sont corrélées (colinéarité), le calcul matriciel pseudo-inverse conduit à des modèles instables. Une autre contrainte importante est que la MLR ne peut pas être calibrée si le nombre d’échantillons est inférieur au nombre de variables. Ces deux limitations sont très souvent rencontrées en spectroscopie ou en imagerie où les variables sont nombreuses et fortement colinéaires. Ainsi, d’autres méthodes de modélisation doivent être adoptées pour ce type de données.
PCR – Principal Component Regression
Afin de pallier aux problèmes inhérents de la méthode MLR, c’est-à-dire la gestion de données colinéaires et/ou de données pour lesquelles le nombre de variables est supérieur au nombre d’échantillons, il est possible de procéder en deux étapes :
- La première étape consiste à appliquer une ACP sur X et à en extraire k composantes informatives (non bruitées)
- Les scores ainsi extraits peuvent alors être utilisés dans une MLR à la place de X
Cette méthode est appelée Régression sur Composantes Principales (PCR). Son inconvénient est que les composantes extraites par l’ACP ne sont pas calculées en fonction de leur lien avec le paramètre y mais uniquement en fonction de la variance maximale de X. Le paramètre y n’étant pas toujours lié aux variations les plus importantes dans X, les modèles ne sont donc pas toujours très performants.
PLS – Partial Least Square Regression
Des méthodes quantitatives, la Régression aux Moindres Carrés (PLS) est la méthode la plus utilisée en chimiométrie.
Plutôt que de calculer les composantes en utilisant uniquement la variance de X, ce que fait l’ACP, la PLS prend en compte la covariance entre les variables X et les variables Y, c’est-à-dire les variances de X et Y et la corrélation entre X et Y. Les composantes, appelées ici variables latentes (LV), sont donc construites de façon à modéliser Y. Cette méthode est donc généralement plus performante que la PCR.
Plus le nombre de variables latentes est faible, plus le modèle est robuste, c’est-à-dire stable vis à vis de perturbations extérieures ,mais plus il risque d’être sous-ajusté. Il est donc nécessaire de bien choisir le nombre de variables latentes afin de créer un modèle performant et robuste.
-
Les méthodes de discrimination supervisée
SIMCA – Soft Independent Modelling of Class Analogy
SIMCA – (Soft Independent Modelling of Class Analogy) est basée sur l’ACP (Analyse en Composantes Principales) et convient donc aux données de grande dimension.
Chaque classe k est modélisée par une ACP spécifique. Cette ACP permet de modéliser la variance intra-classe. Puis, pour chaque modèle, un intervalle de confiance est créé pour définir la limite d’appartenance de la classe. Cette limite peut être basée sur la distance euclidienne des résidus X (notée Q), sur le levier (ou de façon équivalente le T² de Hotelling ou la distance de Mahalanobis) ou, le plus souvent, sur la combinaison de ces deux critères.
Un échantillon inconnu est ensuite classé dans la classe k s’il se situe dans les limites de la classe. Un échantillon peut être affecté à plusieurs classes si elles se chevauchent ou sont très proches les unes des autres, ou bien à aucune des classes et, dans ce cas, il est possible de considérer une « classe de rejet ».
L’avantage de SIMCA par rapport à d’autres méthodes de discrimination est qu’il est très facile de rajouter de nouvelles classes. En effet, les modèles ACP sont réalisés par classe, indépendamment des autres classes.
Cette méthode fonctionne très bien pour l’authentification de produits qui présentent des valeurs X bien différentes. En revanche, lorsque les signaux sont très proches, des méthodes basées sur les différences inter-classes seront préférables.
PLS DA – PLS Discriminant Analysis
La PLS-DA est une méthode dérivée de la PLS qui permet une analyse qualitative ou analyse discriminante.
Comme pour la PLS, la construction du modèle PLS-DA est basée sur la covariance de X et de Y. Mais contrairement à la PLS, les Y de la PLS-DA ne sont pas des valeurs continues. Chaque colonne de Y correspond à une classe et contient 1 si l’échantillon appartient à la classe, ou 0 sinon (codage disjonctif complet).
La PLS-DA se focalise donc sur la séparation des classes contrairement à la méthode SIMCA. En revanche, si les classes sont très hétérogènes cela peut compliquer la modélisation car tous les échantillons de la classe se voient attribuer la même valeur quantitative.
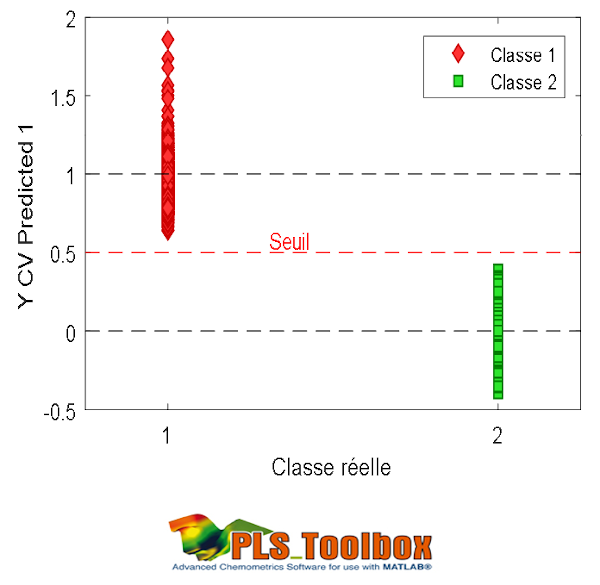
Les prédictions sont des valeurs continues car le modèle reste tout de même une PLS. Un nouvel échantillon sera attribué à la classe si celui-ci présente une prédiction proche de 1 pour la colonne associée. Un seuil est généralement établi pour décider si l’échantillon est attribué ou non à la classe, comme le montre la figure.
-
Les méthodes de Machine Learning
SVM – Support Vector Machines
La méthode des SVM (Support Vector Machines) est la plupart du temps utilisée pour les problématiques non-linéaires ou complexes. Elle est basée sur la recherche de frontières pour la séparation de deux classes. Ainsi, seule une partie des échantillons d’étalonnage est réellement utilisée : il s’agit des vecteurs supports délimitant les frontières.
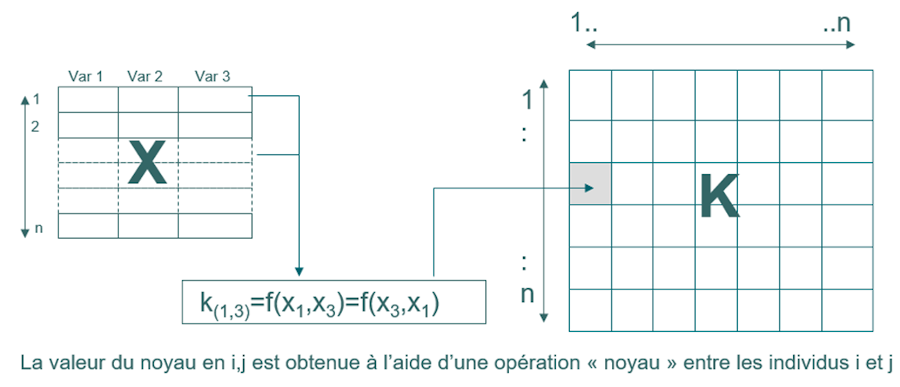
Les données sont transformées dans un nouvel espace, appelé noyau (kernel), qui permet de modéliser la non-linéarité. En étalonnage, cette matrice est de dimension NxN. Le noyau le plus courant est le noyau gaussien qui nécessite un paramètre d’optimisation de la largeur de la gaussienne (sigma) qui permet d’ajuster le degré de linéarité. La méthode SVM nécessite également l’optimisation d’un paramètre de régularisation qui permet d’éviter le sur-apprentissage (C ou cost). Le réglage de ces deux paramètres est crucial pour obtenir un modèle à la fois performant et robuste.
Bien qu’à l’origine créées pour la classification, les SVM ont été étendues à la régression. Il existe notamment deux méthodes : la SVM-R et la LS-SVM.
ANN – Réseaux de Neurones Artificiels
Les réseaux de neurones artificiels (ANN), ou shallow networks (pour les différencier des méthodes de deep learning), sont des outils de modélisation mimant le principe biologique des neurones.
Le Réseau de Neurones Artificiels le plus utilisé est le Multi-Layer Perceptron (MLP). Il est organisé sous formes de couches de neurones interconnectés (fully connected), avec, a minima 3 couches :
- 1 couche d’entrée correspondant aux variables X (1 neurone par colonne)
- 1 ou plusieurs couche(s) cachée(s) de k neurones qui correspondent aux poids qu’il faudra entrainer pour réaliser le modèle
- 1 couche de sortie qui correspond aux Y (1 neurone par colonne).
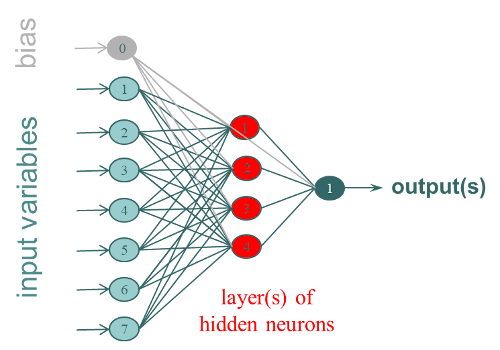
Les Y peuvent correspondre à des valeurs quantitatives à prédire ou à des classes selon le type de réseau développé. Les ANN sont des méthodes non-linéaires stochastiques, c’est-à-dire que chaque processus de modélisation aboutira à un résultat différent, il est généralement conseillé de réaliser plusieurs itérations.
Les non-linéarités sont gérées par l’utilisation de fonctions d’activation à la sortie de chaque neurone de la couche cachée. Ces fonctions d’activation peuvent être de différentes sortes (tangente, sigmoïde, …).
Les poids sont ajustés en parcourant plusieurs fois chaque échantillon de la base d’étalonnage. Un critère d’arrêt est alors nécessaire pour éviter le sur-apprentissage. Ces méthodes sont donc à utiliser avec précaution, mais des astuces de modélisation permettent d’obtenir des modèles robustes.
LWR – Locally Weighted Regression
La Locally Weighted Regression (LWR) peut être utile en cas de non-linéarité, ou lorsque vos données sont hétérogènes ou groupées.
Le principe de cette méthode est de calculer un modèle de régression linéaire pour chaque échantillon, en utilisant uniquement un nombre défini de ses voisins les plus proches sélectionnés au sein de la base de données d’étalonnage plutôt que la population entière :
- Pour un échantillon à prédire, les voisins sont sélectionnés en fonction de leur proximité dans une ACP calculée globalement sur tous les échantillons de la base d’étalonnage (valeurs X).
- La proximité de la réponse à prédire (valeurs Y) pourrait également être prise en compte pour influencer la sélection des échantillons les plus proches. La réponse de l’échantillon à prédire peut être estimée par un modèle global et comparée aux réponses connues des échantillons de la base d’étalonnage.
- Un modèle PLS (ou PCR) local est ensuite construit pour l’échantillon à prédire, en utilisant uniquement les voisins sélectionnés.
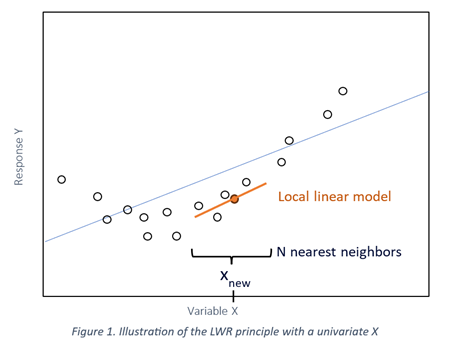
Il en résulte un modèle « linéaire par morceaux » basé sur la plage de X et Y, qui permet de gérer les relations non linéaires entre X et Y.
CART – Classification And Regression Trees
Les modèles CART (Classification And Regression Trees) fonctionnent selon des séparations séquentielles dichotomiques du jeu de données, sous forme d’arbre.
À chaque nœud de l’arbre, une variable est sélectionnée selon son intérêt prédictif, et le seuil optimal de séparation est calculé. Les échantillons ayant une valeur inférieure au seuil sont dirigés sur la gauche de l’arbre et ceux supérieurs ou égaux au seuil sur la droite. Puis, chaque sous-partie est à nouveau divisée en deux à partir d’une nouvelle variable (qui peut être identique ou différente). Ce procédé est réalisé jusqu’à ce que l’ensemble des échantillons se retrouve séparé ou qu’un minimum par feuille (nœud terminal) est atteint.
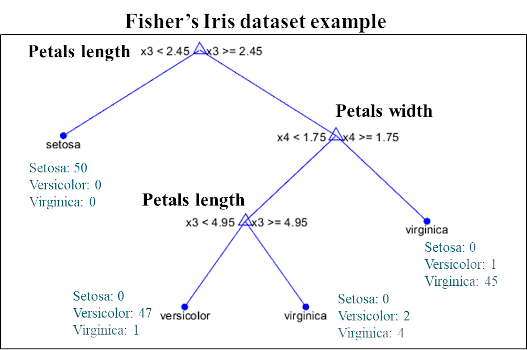
Dans le cas d’un modèle de discrimination, un nouvel échantillon sera attribué à la classe majoritaire de la feuille dans laquelle il tombe après avoir parcouru l’arbre. Dans le cas d’un modèle de régression, la valeur attribuée est la moyenne des échantillons de la feuille.
Random Forests (forêts aléatoires)
Une amélioration de cette approche, les « Random Forests », permet de palier aux problèmes de sur-apprentissage inhérents à la méthode CART.
Le principe est de réaliser plusieurs arbres à partir d’un échantillonnage bootstrap des données initiales, aussi bien sur les échantillons que sur les variables. Lorsqu’un nouvel échantillon est soumis à la forêt, sa prédiction finale correspond à la moyenne des prédictions de l’ensemble des arbres dans le cas d’une prédiction quantitative, et à la classe majoritaire dans le cas d’une classification. Les méthodes basées sur la génération de plusieurs modèles sont regroupées sous le terme des « ensemble methods », les RF en font partie.
Les RF permettent à la fois de modéliser de fortes non-linéarités et de gérer les distributions asymétriques des variables X. Elles permettent également d’utiliser des variables catégorielles en entrée (tout comme CART) en combinaisons des variables quantitatives discrètes ou continues.
Plusieurs paramètres sont à optimiser dont, le nombre d’arbres dans la forêt, le nombre de variables à tirer aléatoirement à chaque nœud, et le nombre d’échantillons minimum par feuille.
Boosting
Les méthodes de Boosting, tout comme les Random Forests, font partie des ensemble methods. En revanche, contrairement aux RF, les modèles de boosting sont réalisés de façon séquentielle.
Les méthodes les plus classiques utilisent des arbres successifs de type CART peu profonds, mais il est possible d’appliquer le même principe avec d’autres méthodes comme par exemple des SVM. La librairie la plus connue est XGBoost, elle regroupe plusieurs méthodes de boosting.
Dans le cas de la régression, on peut citer la méthode LSBoost, dont le principe est de réaliser un premier arbre pour modéliser Y. Le deuxième arbre est ensuite construit afin de prédire le résidu de Y (auquel une partie du Y initial est rajouté de façon à réaliser un apprentissage plus progressif), et ainsi de suite jusqu’à obtenir un nombre suffisant d’arbres pour obtenir un modèle performant.
Dans le cas de la discrimination, l’algorithme AdaBoost procède par pondération des échantillons mal classés. Un premier arbre permet de réaliser une première séparation des classes. Les échantillons mal classés se voient alors attribuer un poids plus important avant de construire l’arbre suivant afin que ce dernier puisse se focaliser sur les échantillons problématiques. Le procédé est répété jusqu’à obtenir un modèle performant.
Les résultats des différents arbres sont combinés pour obtenir la prédiction finale.
-
Les méthodes de Deep Learning
CNN – Convolutional Neural Network
La méthode des Convolutional Neural Networks (CNN) est la plus répandue du domaine du deep learning. Elle fait partie des réseaux de neurones profonds, il y a donc de grandes similarités avec les réseaux de neurones déjà cités plus haut.
Cette méthode a été initialement développée pour la reconnaissance d’images. L’idée est d’ajouter des couches de convolution en amont des couches « classiques » des ANN, dans l’objectif d’extraire automatiquement (par apprentissage) des caractéristiques (features) informatives pour l’objectif recherché. Pour l’analyse d’images, ces couches convolutionnelles (combinées à d’autres paramètres : pooling, reLu, …) permettent de s’affranchir notamment de la position de l’objet et de sa taille dans l’image afin de réaliser des modèles robustes. De nombreux paramètres sont à définir : le nombre et la nature des couches, la taille des filtres, le nombre de neurones des couches cachées, … Elle requiert ainsi un nombre très important d’échantillons pour permettre d’entrainer une très grande quantité de poids sans sur-apprentissage. La complexité de cette méthode en fait cependant un outil très puissant.
Ce type de méthode peut également être étendu à d’autres types de données comme par exemple des données spectroscopiques, en ajustant les paramètres de façon adéquate.
-
Les pré-traitements
Prétraitements spectroscopiques
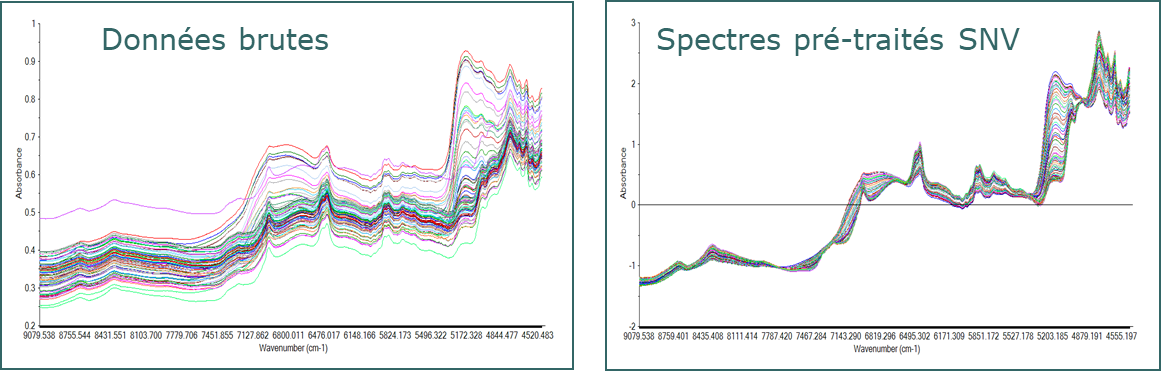
Les données spectroscopiques présentent des particularités qui nécessitent un minimum de savoir-faire avant de pouvoir les utiliser dans un modèle. Elles sont sujettes à des variations de signal dues à des effets indésirables dont la plus répandue est la diffusion de la lumière causée par la structure physique de l’échantillon. Cela est notamment le cas sur les spectres proche infrarouge et dans le domaine du visible. D’autres types de spectroscopies, comme par exemple le Raman, présentent aussi des perturbations indésirables comme la fluorescence, entrainant de fortes lignes de bases masquant les pics informatifs.
Ces variations peuvent être importantes si le paramètre d’intérêt à modéliser est de nature physique (structure de l’échantillon, taille de particules, …), mais elles sont en général indésirables pour la prédiction de propriétés chimiques.
Des méthodes de correction des effets additifs et multiplicatifs sont alors appliquées de façon à atténuer ces effets indésirables et ainsi aider les modèles à se focaliser sur la partie informative dans le spectre.
Dans les prétraitements les plus connus on retrouvera notamment : les corrections de ligne de base (detrend), la Standard Normal Variate (SNV), la Multiplicative Scatter Correction (MSC), les dérivées première et seconde (Savitzky-Golay, Norris Gap), le lissage pour diminuer le bruit, …
D’autres méthodes plus avancées peuvent également être utilisées : l’Extended-MSC (EMSC), les méthodes d’orthogonalisation (EPO, EROS, DOP, …), …
Réduction de dimensions
Les signaux spectraux sont de nature continue et sont donc colinéaires. Ils présentent également très souvent un très grand nombre de variables. Certaines méthodes ne seront donc pas appropriées, comme par exemple la MLR ou encore des méthodes pour lesquelles le sur-apprentissage peut être critique si le nombre de variables est important comme par exemple les ANN (plus de poids à entrainer). Il est ainsi assez courant d’appliquer des méthodes de réduction de dimensions avant d’utiliser ce type de modèles.
La plus simple étant d’appliquer une ACP et d’en extraire k composantes, supposées informatives (non bruitées). Ces composantes étant ensuite utilisées comme variables prédictives dans la méthode choisie.
Il est également possible de réaliser par exemple une PLS ou une PLS-DA (selon si l’on souhaite réaliser un modèle de régression quantitative ou une discrimination), de façon à extraire des composantes plus informatives que celle issues d’une ACP.
Sélection de variables
La sélection de variables peut avoir plusieurs avantages dont notamment :
- Principe de parcimonie : un modèle moins complexe est un modèle plus robuste
- Peut faire office de méthode de réduction de dimensions (attention tout de même à la méthode utilisée par la suite si les longueurs d’onde extraites sont corrélées entre elles)
- Permet de conserver uniquement les longueurs d’onde ou les plages de longueur d’onde informatives et non bruitées. Cela simplifie le modèle et peut le rendre plus performant du fait de l’élimination de zones indésirables
- Peut permettre de choisir quelques longueurs d’onde pour développer un instrument multi-spectral plus simple
La méthode la plus efficace serait de pouvoir tester toutes les combinaisons de variables possibles. Malgré les avancées au niveau des puissances de calcul des ordinateurs, ce procédé n’est pas réellement envisageable si le nombre de variables est important. Des stratégies doivent alors être mises en place afin de diminuer le nombre de combinaisons à tester. Quelques méthodes sont citées à titre d’exemples mais il existe de nombreuses autres méthodes de sélection de variables.
-
La sélection pas à pas
La sélection de variables pas à pas (ou stepwise) peut être réalisée soit de façon forward en sélectionnant une à une les variables informatives, soit de façon backward en éliminant une à une les variables non informatives, soit en combinant les deux approches.
Dans le cas de la sélection forward, le principe est de réaliser un modèle sur chacune des variables, et celle aboutissant aux meilleures performances est sélectionnée. A l’étape suivante, la combinaison 2 à 2 de cette première variable avec toutes les autres variables permet de sélectionner une deuxième variable, … On procède ainsi jusqu’à sélectionner k variables ou jusqu’à ce que les performances atteignent un minimum.
Dans le cas de l’interval-PLS (iPLS) on privilégie généralement la sélection de bandes spectrales contiguës plutôt que des longueurs d’onde isolées. Tout dépend bien entendu de l’objectif recherché.
-
Les algorithmes génétiques
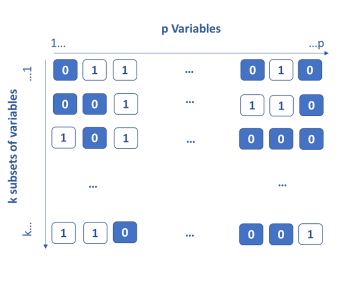
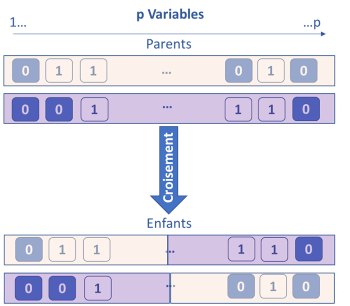
La méthode des algorithmes génétiques est une méthode basée sur le principe de l’évolution darwinienne. L’idée est de considérer que chaque variable possède k gènes qui sont, soit activés (1), soit désactivés (0). Au démarrage, les gènes sont activés de façon aléatoire, puis k modèles sont réalisés sur les k subsets de variables actives. Les k/2 subsets de variables les moins performants sont éliminés. Pour les k/2 restants, des croisements sont réalisés en interchangeant des portions de gènes entre eux (single ou double cross-over breedings).
Chaque subset est également soumis à une probabilité de mutation aléatoire en activant ou désactivant certaines variables. A la fin de cette étape, à nouveau k subsets sont obtenus et ré-évalués. Ce procédé est itéré jusqu’à l’obtention du critère d’arrêt. Au fil des itérations, les variables les plus informatives sont identifiées et conservées.
Il est possible de considérer des zones spectrales à la place de variables uniques dans le cas de données spectroscopiques.
Cette méthode est une méthode stochastique. Ainsi, à chaque fois que la méthode est lancée, un résultat différent peut être obtenu.
-
Les méthodes de supervision de procédés
MSPC – Multivariate Statistical Process Control
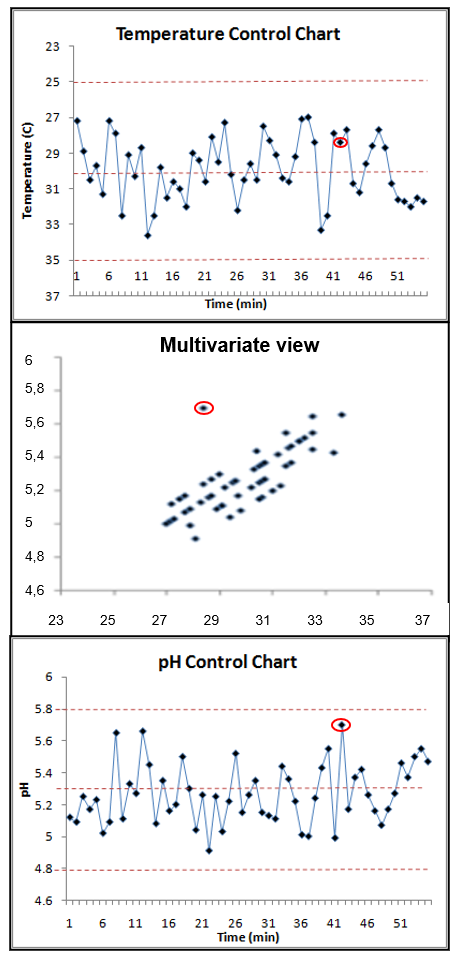
Les méthodes de Maîtrise Statistique de Procédés (MSP ou ou Statistical Process Control – SPC) sont largement utilisées dans le but de suivre un procédé et de détecter d’éventuelles anomalies ou dérives. La SPC a cependant l’inconvénient de ne regarder qu’un seul paramètre à la fois, ce qui rend le contrôle compliqué si le nombre de paramètres à suivre est important; mais cette méthode est également moins fiable car elle ne prend pas en compte les interactions entre les diverses variables du procédé.
La MSPC (Multivariate Statistical Process Control) permet de contrôler les procédés de façon multivariée en prenant ainsi en compte la globalité du procédé. Elle est généralement basée sur l’ACP, mais d’autres méthodes peuvent également être utilisées. Les statistiques de levier et de résidus sont suivies afin de détecter d’éventuels problèmes. Les valeurs au-delà des intervalles de confiance statistiques sont considérées comme des anomalies. Il est ensuite possible de revenir sur la ou les variable(s) à l’origine de l’anomalie afin de diagnostiquer le problème et de pouvoir intervenir rapidement sur le procédé.
La MSPC peut être réalisée sur des données spectroscopiques (Proche infrarouge, Raman, …), paramètres procédés (température; pression) ou analytiques (concentrations, …), ou bien sur une combinaison des deux.
BSPC – Batch Statistical Process Control
La BSPC (Batch Statistical Process Control) est l’équivalent de la MSPC mais pour le contrôle de procédés en batch. Le système est donc plus complexe.
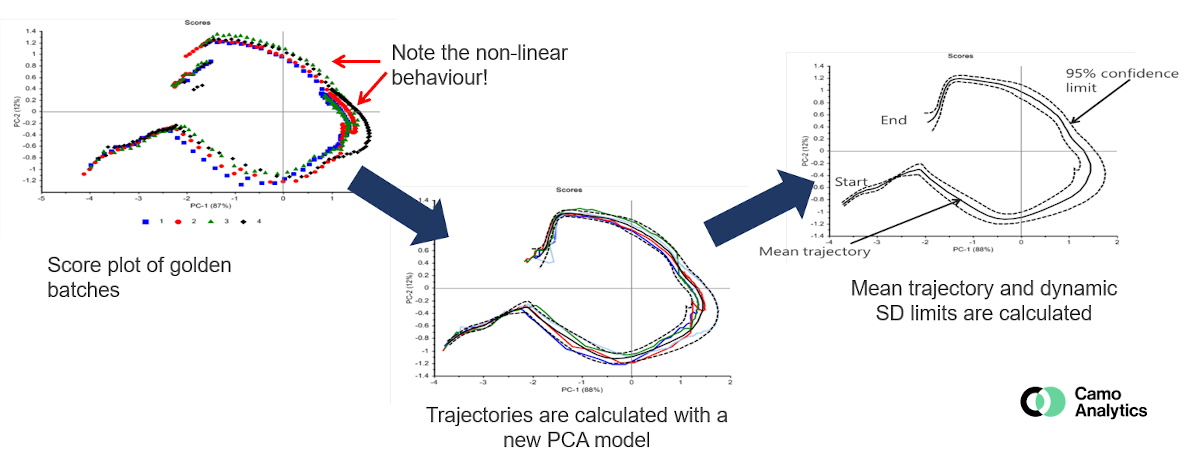
La méthode la plus classique est généralement de comparer les nouveaux batch à un « golden batchs », qui représente un lot de référence pour lequel les conditions sont maitrisées et optimales. Ce « golden batch » représente la trajectoire idéale ou standard. Les batchs déviant de cette trajectoire peuvent ainsi être détectés, de la même façon que pour un modèle MSPC en suivant les scores, et/ou les résidus et le levier. Il doit donc être bien défini à partir de plusieurs batchs réalisés en conditions standard afin de réaliser un modèle robuste avec des intervalles de confiance pertinents.
Bien que l’ACP soit la méthode la plus courante, des méthodes multivoies peuvent également être utilisées pour suivre le procédé, comme par exemple la méthode PARAFAC, les données sont en effet de nature organisées en 3 dimensions : batch x temps x variables.
La BSPC fait appel à divers challenges en termes de traitement de données, dont notamment le recalage temporel des batchs de façon à bien pouvoir les comparer entre eux (durée différente, étapes-clés intervenant à différents moments dans le temps, …). Plusieurs méthodes permettent de gérer ce problème selon le cas étudié : synchronisation, déformation temporelle, normalisation, index de maturité, …. Cette étape est cruciale lorsque l’objectif est de comparer à un « golden batch » et/ou lorsque des méthodes multivoies sont utilisées.
-
Les plans d’expériences
Plans d’expériences
L’utilisation de bases de données historiques pour modéliser des processus nécessite un très grand nombre d’observations pour assurer un minimum de variabilité. Lorsque cela est possible, une méthode plus rationnelle consiste à choisir certaines observations ou expériences pour couvrir l’ensemble des conditions de fonctionnement souhaitées, c’est-à-dire l’espace de conception, avec un maximum de variabilité. Les plans d’expériences (plans expérimentaux) sont les outils de chimiométrie qui visent à planifier les expériences pertinentes, à minimiser les coûts sans nuire à la qualité de l’information, à quantifier les différents effets factoriels, à modéliser et à optimiser les processus.
Différents plans d’expériences correspondent à différents objectifs:
– La méthodologie comprend souvent une première étape qui consiste à réaliser un plan de criblage. Les expériences sont choisies afin de quantifier et sélectionner les facteurs d’influence parmi un grand nombre de facteurs.
– Les plans factoriels complets sont les plans de base qui réalisent toutes les expériences possibles avec k facteurs à deux niveaux, bas et haut. Toutes les expériences aux limites de l’espace de conception sont planifiées
– Les plans factoriels fractionnaires sont utilisés pour sélectionner les facteurs lorsque le nombre d’expériences doit être réduit. Le principe permet de sélectionner les expériences de la conception factorielle complète qui doivent être exécutées sans perte d’information significative
– Enfin des plans d’expériences utilisant des modèles linéaires sont également couramment utilisés pour identifier les quelques facteurs significatifs parmi de nombreux autres : les plans de Plackett-Burman, les conceptions de dépistage de Rechtschaffner… »
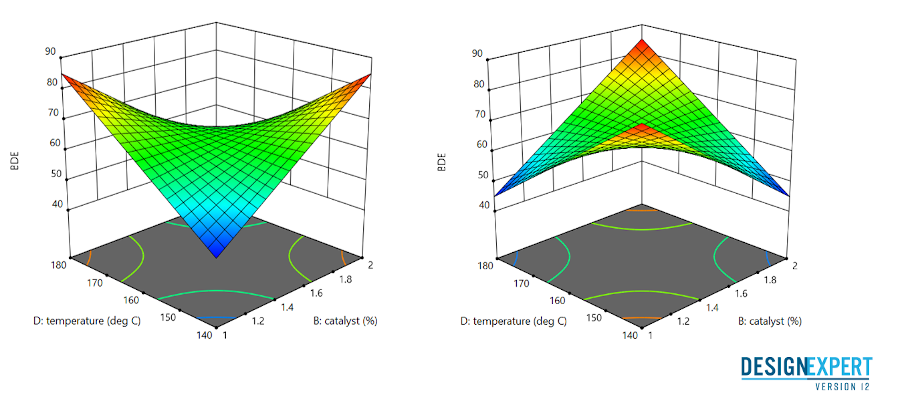
– Les plans d’optimisation servent à modéliser plus précisément les procédés ainsi que leurs non-linéarités éventuelles. Les plans d’optimisation les plus utilisés sont les plans centrés composites.
Ils en parlent
« Ondalys, un pont entre la recherche universitaire et l’industrie »
Notre expertise au service de l’analyse de vos données
Fort d’une expérience de plus de 15 ans dans l’analyse de données (chimiométrie), en particulier appliquée aux mesures spectroscopiques, analytiques et sensorielles, nos équipes vous accompagnent à chaque étape de vos projets
Besoin d’une formation sur mesure ?
Nos équipes étudient votre demande plus en détails pour vous proposer une formation personnalisée
